| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 14.1 | Example 1 to 4 (Before Exercise 14.2) | Exercise 14.2 |
| Example 5 to 9 (Before Exercise 14.3) | Exercise 14.3 | Example 10 to 15 (Before Exercise 14.4) |
| Exercise 14.4 | ||
Chapter 14 Statistics
Welcome to the solutions guide for Chapter 14: Statistics. This crucial chapter significantly enhances our ability to handle, interpret, and present numerical information, building upon the foundational concepts introduced in Class 8. Statistics is the science of collecting, organizing, analyzing, interpreting, and presenting data. In this chapter, we delve deeper into methods for systematically organizing raw data into meaningful formats and explore powerful techniques for visualizing data patterns through various graphs. Furthermore, we are introduced to fundamental methods for summarizing data sets using single representative values known as measures of central tendency, specifically the mean, median, and mode, primarily focusing on their calculation for ungrouped data.
The initial focus lies on the collection and presentation of data. Raw data, in its unprocessed form, can be overwhelming and difficult to interpret. Therefore, solutions emphasize the importance of organizing data into frequency distribution tables. This involves tallying occurrences (frequency) of data points, which can be done for individual values (ungrouped frequency distribution) or by grouping data into class intervals (grouped frequency distribution). Key concepts associated with grouped data, such as defining appropriate class intervals, calculating class marks (midpoints of intervals, $Class Mark = \frac{\text{Upper Limit + Lower Limit}}{2}$), and understanding cumulative frequency, are thoroughly explained.
A significant portion of this chapter is dedicated to the graphical representation of data, as visual aids often provide intuitive insights into data trends. The solutions provide detailed, step-by-step instructions for constructing various graphical forms:
- Bar Graphs: Primarily used for comparing discrete categories or items, revisiting their construction and interpretation.
- Histograms: Specifically designed for representing grouped continuous data. Solutions emphasize the key features: bars are drawn adjacent to each other (no gaps), the width of bars represents the class interval, and the height corresponds to the frequency. Importantly, constructing histograms for data with uniform width intervals versus those with varying width intervals is addressed, explaining the need to adjust bar heights proportionally (using frequency density) in the latter case to ensure area represents frequency accurately.
- Frequency Polygons: A line graph representation of frequency distribution. Solutions demonstrate two primary construction methods: either by joining the mid-points of the tops of the bars in a histogram or, more directly, by plotting the frequency against the class mark for each interval and connecting these points with straight line segments. It's crucial to close the polygon by joining the first and last points to the class marks of hypothetical intervals with zero frequency at both ends.
Following data presentation, the focus shifts to data analysis using measures of central tendency for ungrouped data. These measures provide a single value summarizing the "center" or typical value of a dataset. The solutions detail the calculation for:
- Mean (or Arithmetic Average): Calculated as the sum of all observations divided by the total number of observations. The formula is $\bar{x} = \frac{\sum\limits_{i=1}^{n} x_i}{n}$.
- Median: The middle value of the dataset when arranged in ascending or descending order. Solutions explain how to find it for both an odd number of observations (the direct middle value) and an even number of observations (the average of the two middle values).
- Mode: The value that appears most frequently in the dataset. A dataset can have one mode (unimodal), two modes (bimodal), or more (multimodal).
While the detailed calculation of these measures for grouped data is typically introduced in Class 10, this chapter lays the essential groundwork. The solutions consistently emphasize the importance of selecting the most appropriate graphical representation for a given dataset and interpreting what each measure of central tendency reveals about the data's characteristics, fostering effective data summarization and understanding.
Exercise 14.1
Question 1. Give five examples of data that you can collect from your day-to-day life.
Answer:
Here are five examples of data that can be collected from our day-to-day life:
1. The number of hours you sleep each night over a week.
2. The amount of money you spend each day for a month.
3. The temperature recorded at a specific time each day for a week.
4. The number of students present in your class each day.
5. The time taken to travel from home to school each morning.
Question 2. Classify the data in Q.1 above as primary or secondary data.
Answer:
Based on the definition of primary and secondary data:
Primary Data: Data collected by the investigator himself for a specific purpose.
Secondary Data: Data which has been collected by someone else for some other purpose.
All five examples of data given in Q.1 are collected by the person observing or experiencing them directly for their own use.
Therefore, all the data collected in Q.1 are examples of Primary Data.
Example 1 to 4 (Before Exercise 14.2)
Example 1. Consider the marks obtained by 10 students in a mathematics test as given below:
| 55 | 36 | 95 | 73 | 60 | 42 | 25 | 78 | 75 | 62 |
Answer:
Given
The marks obtained by 10 students in a mathematics test are:
55, 36, 95, 73, 60, 42, 25, 78, 75, 62
This form of data is known as raw data.
Solution
To analyze the given data, we first arrange the marks in ascending order. This helps in understanding the distribution and calculating various statistical measures.
The marks in ascending order are:
25, 36, 42, 55, 60, 62, 73, 75, 78, 95
Now, let's calculate some common statistical measures for this data.
1. Range of the Data
The range is the difference between the highest and the lowest values in the data set.
Highest marks = 95
Lowest marks = 25
Range = Highest marks - Lowest marks
Range = $95 - 25 = 70$
So, the range of the marks is 70.
2. Mean of the Data
The mean (or average) is the sum of all the observations divided by the total number of observations.
The formula for the mean is: Mean ($\bar{x}$) = $\frac{\text{Sum of all observations}}{\text{Number of observations}}$
Sum of marks = $25 + 36 + 42 + 55 + 60 + 62 + 73 + 75 + 78 + 95 \ $$ = 591$
Number of students ($n$) = 10
Mean = $\frac{591}{10} = 59.1$
So, the mean marks of the students is 59.1.
3. Median of the Data
The median is the middle value of a data set when it is arranged in ascending or descending order.
The arranged data is: 25, 36, 42, 55, 60, 62, 73, 75, 78, 95.
The number of observations ($n$) is 10, which is an even number.
For an even number of observations, the median is the average of the two middle terms, which are the $(\frac{n}{2})^{th}$ term and the $(\frac{n}{2} + 1)^{th}$ term.
$(\frac{10}{2})^{th}$ term = $5^{th}$ term
$(\frac{10}{2} + 1)^{th}$ term = $6^{th}$ term
From the arranged data, the $5^{th}$ term is 60 and the $6^{th}$ term is 62.
Median = $\frac{5^{th} \text{ term} + 6^{th} \text{ term}}{2}$
Median = $\frac{60 + 62}{2} = \frac{122}{2} = 61$
So, the median of the marks is 61.
4. Mode of the Data
The mode is the value that appears most frequently in the data set.
Looking at the data: 25, 36, 42, 55, 60, 62, 73, 75, 78, 95.
Each mark appears only once. Since no value is repeated, there is no mode for this data set.
Example 2. Consider the marks obtained (out of 100 marks) by 30 students of Class IX of a school:
Prepare an ungrouped frequency distribution table on the basis of the above data using tally marks.
| 10 | 20 | 36 | 92 | 95 | 40 | 50 | 56 | 60 | 70 |
| 92 | 88 | 80 | 70 | 72 | 70 | 36 | 40 | 36 | 40 |
| 92 | 40 | 50 | 50 | 56 | 60 | 70 | 60 | 60 | 88 |
Answer:
The given data represents the marks obtained by 30 students.
To prepare an ungrouped frequency distribution table, we list each unique mark and count how many times it appears in the data using tally marks.
Here is the ungrouped frequency distribution table:
| Marks | Tally Marks | Frequency |
| 10 | | | 1 |
| 20 | | | 1 |
| 36 | ||| | 3 |
| 40 | |||| | 4 |
| 50 | ||| | 3 |
| 56 | || | 2 |
| 60 | |||| | 4 |
| 70 | |||| | 4 |
| 72 | | | 1 |
| 80 | | | 1 |
| 88 | || | 2 |
| 92 | ||| | 3 |
| 95 | | | 1 |
| Total | 30 |
Example 3. 100 plants each were planted in 100 schools during Van Mahotsava. After one month, the number of plants that survived were recorded as :
| 95 | 67 | 28 | 32 | 65 | 65 | 69 | 33 | 98 | 96 |
| 76 | 42 | 32 | 38 | 42 | 40 | 40 | 69 | 95 | 92 |
| 75 | 83 | 76 | 83 | 85 | 62 | 37 | 65 | 63 | 42 |
| 89 | 65 | 73 | 81 | 49 | 52 | 64 | 76 | 83 | 92 |
| 93 | 68 | 52 | 79 | 81 | 83 | 59 | 82 | 75 | 82 |
| 86 | 90 | 44 | 62 | 31 | 36 | 38 | 42 | 39 | 83 |
| 87 | 56 | 58 | 23 | 35 | 76 | 83 | 85 | 30 | 68 |
| 69 | 83 | 86 | 43 | 45 | 39 | 83 | 75 | 66 | 83 |
| 92 | 75 | 89 | 66 | 91 | 27 | 88 | 89 | 93 | 42 |
| 53 | 69 | 90 | 55 | 66 | 49 | 52 | 83 | 34 | 36 |
Prepare an grouped frequency distribution table on the basis of the above data using tally marks.
Answer:
Given
The number of plants that survived in 100 schools are given as raw data. The total number of observations is 100.
To Do
Prepare a grouped frequency distribution table for the given data using tally marks.
Solution
To create a grouped frequency distribution table, we first need to determine the range of the data and decide on suitable class intervals.
Step 1: Find the range of the data.
First, let's identify the minimum and maximum values in the dataset.
By observing the data:
Maximum value = 98
Minimum value = 23
Range = Maximum value - Minimum value = $98 - 23 = 75$
Step 2: Decide on the class intervals.
Since the data ranges from 23 to 98, we can create class intervals of size 10 to organize the data effectively. We can start the first interval from 20 to cover all the values. The class intervals will be 20-29, 30-39, 40-49, and so on, up to 90-99.
Step 3: Tally the data.
We will now go through the data and place a tally mark ($|$) against the corresponding class interval for each value. A group of five tally marks is represented as $\bcancel{||||}$.
After going through all 100 data points, we count the tally marks for each class to get the frequency.
The resulting grouped frequency distribution table is as follows:
| Class Interval (Number of survived plants) | Tally Marks | Frequency (Number of schools) |
| 20 - 29 | $|||$ | 3 |
| 30 - 39 | $\bcancel{||||} \; \bcancel{||||} \; ||||$ | 14 |
| 40 - 49 | $\bcancel{||||} \; \bcancel{||||} \; ||$ | 12 |
| 50 - 59 | $\bcancel{||||} \; |||$ | 8 |
| 60 - 69 | $\bcancel{||||} \; \bcancel{||||} \; \bcancel{||||} \; |||$ | 18 |
| 70 - 79 | $\bcancel{||||} \; \bcancel{||||}$ | 10 |
| 80 - 89 | $\bcancel{||||} \; \bcancel{||||} \; \bcancel{||||} \; \bcancel{||||} \; |||$ | 23 |
| 90 - 99 | $\bcancel{||||} \; \bcancel{||||} \; ||$ | 12 |
| Total | 100 |
This table presents the given data in a grouped format, showing how many schools fall into each category of surviving plants.
Example 4. Let us now consider the following frequency distribution table which gives the weights of 38 students of a class:
Table 14.3
| Weights (in kg) | Number of students |
| 31 - 35 | 9 |
| 36 - 40 | 5 |
| 41 - 45 | 14 |
| 46 - 50 | 3 |
| 51 - 55 | 1 |
| 56 - 60 | 2 |
| 61 - 65 | 2 |
| 66 - 70 | 1 |
| 71 - 75 | 1 |
| Total | 38 |
Prepare continuous and discontinuous grouped frequency distribution table on the basis of the above data.
Answer:
The given table is a grouped frequency distribution table.
This table has class intervals like 31-35, 36-40, etc.
In these intervals, the upper limit of one class (e.g., 35) does not match the lower limit of the next class (e.g., 36).
This type of frequency distribution is called a discontinuous or inclusive grouped frequency distribution.
Discontinuous Grouped Frequency Distribution Table:
| Weights (in kg) | Number of students (Frequency) |
| 31 - 35 | 9 |
| 36 - 40 | 5 |
| 41 - 45 | 14 |
| 46 - 50 | 3 |
| 51 - 55 | 1 |
| 56 - 60 | 2 |
| 61 - 65 | 2 |
| 66 - 70 | 1 |
| 71 - 75 | 1 |
| Total | 38 |
To prepare a continuous grouped frequency distribution table, the upper limit of each class must coincide with the lower limit of the succeeding class.
We find the difference between the upper limit of any class and the lower limit of the next class.
Difference = Lower limit of next class - Upper limit of current class
Using the first two classes (31-35 and 36-40):
Difference = $36 - 35 = 1$
We divide this difference by 2 to get the adjustment factor.
Adjustment factor = Difference / 2 = $1 / 2 = 0.5$
To make the classes continuous, we subtract this adjustment factor from the lower limit of each class and add it to the upper limit of each class.
- New lower limit = Original lower limit - 0.5
- New upper limit = Original upper limit + 0.5
Continuous Grouped Frequency Distribution Table:
| Weights (in kg) (Continuous Class Intervals) | Number of students (Frequency) |
| 30.5 - 35.5 | 9 |
| 35.5 - 40.5 | 5 |
| 40.5 - 45.5 | 14 |
| 45.5 - 50.5 | 3 |
| 50.5 - 55.5 | 1 |
| 55.5 - 60.5 | 2 |
| 60.5 - 65.5 | 2 |
| 65.5 - 70.5 | 1 |
| 70.5 - 75.5 | 1 |
| Total | 38 |
Exercise 14.2
Question 1. The blood groups of 30 students of Class VIII are recorded as follows:
Represent this data in the form of a frequency distribution table. Which is the most common, and which is the rarest, blood group among these students?
| A | B | O | O | AB | O | A | O | B | A | O | B | A | O | O |
| A | AB | O | A | A | O | O | AB | B | A | O | B | A | B | O |
Answer:
Given:
The blood groups of 30 students of Class VIII are recorded as:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O
To Find:
- Frequency distribution table of the blood groups.
- The most common blood group.
- The rarest blood group.
Solution:
We will count the frequency of each blood group from the given data:
- Blood group A: 9 students
- Blood group B: 6 students
- Blood group O: 12 students
- Blood group AB: 3 students
Total number of students = $9 + 6 + 12 + 3 = 30$.
Here is the frequency distribution table for the given data:
| Blood Group | Number of Students (Frequency) |
| A | 9 |
| B | 6 |
| O | 12 |
| AB | 3 |
| Total | 30 |
From the frequency distribution table:
The highest frequency is 12, which corresponds to Blood Group O.
The lowest frequency is 3, which corresponds to Blood Group AB.
Therefore:
The most common blood group among these students is O.
The rarest blood group among these students is AB.
Question 2. The distance (in km) of 40 engineers from their residence to their place of work were found as follows:
| 5 | 3 | 10 | 20 | 25 | 11 | 13 | 7 | 12 | 31 |
| 19 | 10 | 12 | 17 | 18 | 11 | 32 | 17 | 16 | 2 |
| 7 | 9 | 7 | 8 | 3 | 5 | 12 | 15 | 18 | 3 |
| 12 | 14 | 2 | 9 | 6 | 15 | 15 | 7 | 6 | 12 |
Construct a grouped frequency distribution table with class size 5 for the data given above taking the first interval as 0-5 (5 not included). What main features do you observe from this tabular representation?
Answer:
Given:
The distance (in km) of 40 engineers from their residence to their place of work.
Data: 5, 3, 10, 20, 25, 11, 13, 7, 12, 31, 19, 10, 12, 17, 18, 11, 32, 17, 16, 2, 7, 9, 7, 8, 3, 5, 12, 15, 18, 3, 12, 14, 2, 9, 6, 15, 15, 7, 6, 12.
To Construct:
A grouped frequency distribution table with class size 5, taking the first interval as 0-5 (5 not included).
To Find:
Main features observed from the table.
Solution:
We need to group the data into class intervals of size 5. The first interval is given as 0-5, where 5 is not included. This implies the class intervals are $0 \leq d < 5$, $5 \leq d < 10$, $10 \leq d < 15$, and so on, until the maximum value is covered. The maximum value in the data is 32, so we need intervals up to 35.
The class intervals will be: 0-5, 5-10, 10-15, 15-20, 20-25, 25-30, 30-35.
Now, we count the number of engineers falling into each class interval.
- 0-5: Distances $\geq 0$ and $< 5$. The values are 3, 3, 2, 3, 2. Frequency = 5.
- 5-10: Distances $\geq 5$ and $< 10$. The values are 5, 7, 10 (no, 10 is not included), 7, 8, 5, 7, 6, 9, 7, 6, 9. The values are 5, 7, 7, 8, 5, 7, 9, 6, 7, 6, 9. Frequency = 11.
- 10-15: Distances $\geq 10$ and $< 15$. The values are 10, 11, 13, 12, 10, 12, 11, 12, 12, 14, 12. Frequency = 11.
- 15-20: Distances $\geq 15$ and $< 20$. The values are 19, 17, 18, 17, 16, 15, 18, 15, 15. Frequency = 9.
- 20-25: Distances $\geq 20$ and $< 25$. The value is 20. Frequency = 1.
- 25-30: Distances $\geq 25$ and $< 30$. The value is 25. Frequency = 1.
- 30-35: Distances $\geq 30$ and $< 35$. The values are 31, 32. Frequency = 2.
Total frequency = $5 + 11 + 11 + 9 + 1 + 1 + 2 = 40$. This matches the total number of engineers.
Here is the grouped frequency distribution table:
| Distance (in km) | Frequency (Number of engineers) |
| 0 - 5 | 5 |
| 5 - 10 | 11 |
| 10 - 15 | 11 |
| 15 - 20 | 9 |
| 20 - 25 | 1 |
| 25 - 30 | 1 |
| 30 - 35 | 2 |
| Total | 40 |
Main features observed from the tabular representation:
1. The data is concentrated in the smaller distance intervals. A large number of engineers live within 15 km of their workplace ($5 + 11 + 11 = 27$ engineers).
2. Most engineers (11 in 5-10 km and 11 in 10-15 km, totaling 22) live between 5 km and 15 km (excluding 15 km) from their workplace.
3. Only a few engineers (1 in 20-25 km, 1 in 25-30 km, 2 in 30-35 km, totaling 4) live 20 km or more away from their workplace.
Question 3. The relative humidity (in %) of a certain city for a month of 30 days was as follows:
| 98.1 | 98.6 | 99.2 | 90.3 | 86.5 | 95.3 | 92.9 | 96.3 | 94.2 | 95.1 |
| 89.2 | 92.3 | 97.1 | 93.5 | 92.7 | 95.1 | 97.2 | 93.3 | 95.2 | 97.3 |
| 96.2 | 92.1 | 84.9 | 90.2 | 95.7 | 98.3 | 97.3 | 96.1 | 92.1 | 89 |
(i) Construct a grouped frequency distribution table with classes 84 - 86, 86 - 88, etc.
(ii) Which month or season do you think this data is about?
(iii) What is the range of this data?
Answer:
Given:
Relative humidity (in %) of a certain city for a month of 30 days.
Data: 98.1, 98.6, 99.2, 90.3, 86.5, 95.3, 92.9, 96.3, 94.2, 95.1, 89.2, 92.3, 97.1, 93.5, 92.7, 95.1, 97.2, 93.3, 95.2, 97.3, 96.2, 92.1, 84.9, 90.2, 95.7, 98.3, 97.3, 96.1, 92.1, 89.
(i) Construct a grouped frequency distribution table with classes 84 - 86, 86 - 88, etc.
We need to group the data into class intervals of size 2, starting from 84-86. The class intervals are of the form [Lower limit, Upper limit), meaning the lower limit is included, and the upper limit is not included.
The classes will be 84-86, 86-88, 88-90, 90-92, 92-94, 94-96, 96-98, 98-100.
Now, we count the frequency for each class interval:
- 84 - 86: Values $\geq 84$ and $< 86$. Value: 84.9 (1)
- 86 - 88: Values $\geq 86$ and $< 88$. Value: 86.5 (1)
- 88 - 90: Values $\geq 88$ and $< 90$. Values: 89.2, 89 (2)
- 90 - 92: Values $\geq 90$ and $< 92$. Values: 90.3, 90.2 (2)
- 92 - 94: Values $\geq 92$ and $< 94$. Values: 92.9, 92.3, 93.5, 92.7, 93.3, 92.1, 92.1 (7)
- 94 - 96: Values $\geq 94$ and $< 96$. Values: 95.3, 94.2, 95.1, 95.1, 95.2, 95.7 (6)
- 96 - 98: Values $\geq 96$ and $< 98$. Values: 96.3, 97.1, 97.2, 97.3, 96.2, 97.3, 96.1 (7)
- 98 - 100: Values $\geq 98$ and $< 100$. Values: 98.1, 98.6, 99.2, 98.3 (4)
Total frequency = $1 + 1 + 2 + 2 + 7 + 6 + 7 + 4 = 30$.
Here is the grouped frequency distribution table:
| Relative Humidity (in %) | Number of Days (Frequency) |
| 84 - 86 | 1 |
| 86 - 88 | 1 |
| 88 - 90 | 2 |
| 90 - 92 | 2 |
| 92 - 94 | 7 |
| 94 - 96 | 6 |
| 96 - 98 | 7 |
| 98 - 100 | 4 |
| Total | 30 |
(ii) Which month or season do you think this data is about?
The relative humidity values are very high (mostly above 90%). This level of humidity is typically observed during the rainy season (monsoon).
(iii) What is the range of this data?
The range of the data is the difference between the maximum and minimum values in the dataset.
Maximum value = 99.2
Minimum value = 84.9
Range = Maximum value - Minimum value
Range = $99.2 - 84.9$
Range = $14.3$
Question 4. The heights of 50 students, measured to the nearest centimetres, have been found to be as follows:
| 161 | 150 | 154 | 165 | 168 | 161 | 154 | 162 | 150 | 151 |
| 162 | 164 | 171 | 165 | 158 | 154 | 156 | 172 | 160 | 170 |
| 153 | 159 | 161 | 170 | 162 | 165 | 166 | 168 | 165 | 164 |
| 154 | 152 | 153 | 156 | 158 | 162 | 160 | 161 | 173 | 166 |
| 161 | 159 | 162 | 167 | 168 | 159 | 158 | 153 | 154 | 159 |
(i) Represent the data given above by a grouped frequency distribution table, taking the class intervals as 160 - 165, 165 - 170, etc.
(ii) What can you conclude about their heights from the table?
Answer:
Given:
The heights (in cm) of 50 students.
Data: 161, 150, 154, 165, 168, 161, 154, 162, 150, 151, 162, 164, 171, 165, 158, 154, 156, 172, 160, 170, 153, 159, 161, 170, 162, 165, 166, 168, 165, 164, 154, 152, 153, 156, 158, 162, 160, 161, 173, 166, 161, 159, 162, 167, 168, 159, 158, 153, 154, 159.
(i) Represent the data by a grouped frequency distribution table.
We need to construct a grouped frequency distribution table with class intervals 160 - 165, 165 - 170, etc. Since heights are measured to the nearest centimetre and the class boundaries meet (165, 165), these are continuous class intervals of the form [Lower limit, Upper limit), where the lower limit is included, and the upper limit is not included.
First, find the minimum and maximum values in the data.
Minimum height = 150 cm
Maximum height = 173 cm
With a class size of 5 and intervals starting around the minimum value to reach the maximum, the required class intervals are:
[150, 155), [155, 160), [160, 165), [165, 170), [170, 175)
Now, we count the frequency of heights falling in each interval:
- 150 - 155: Heights $\geq 150$ and $< 155$. Values are 150, 154, 150, 151, 154, 153, 154, 152, 153, 154, 153, 154. Count = 12.
- 155 - 160: Heights $\geq 155$ and $< 160$. Values are 158, 156, 158, 156, 158, 159, 159, 158, 159, 159. Count = 10.
- 160 - 165: Heights $\geq 160$ and $< 165$. Values are 161, 161, 162, 162, 164, 160, 162, 164, 160, 161, 162, 161, 162, 161. Count = 14.
- 165 - 170: Heights $\geq 165$ and $< 170$. Values are 165, 168, 165, 165, 166, 168, 165, 166, 167, 168. Count = 10.
- 170 - 175: Heights $\geq 170$ and $< 175$. Values are 171, 172, 170, 170, 173. Count = 5.
Total frequency = $12 + 10 + 14 + 10 + 5 = 51$. Oh, let's recount from the list. 150: 2, 151: 1, 152: 1, 153: 3, 154: 5. Total [150, 155) = 12. 156: 2, 158: 3, 159: 4. Total [155, 160) = 9. 160: 2, 161: 5, 162: 5, 164: 2. Total [160, 165) = 14. 165: 4, 166: 2, 167: 1, 168: 3. Total [165, 170) = 10. 170: 2, 171: 1, 172: 1, 173: 1. Total [170, 175) = 5. Total sum = $12 + 9 + 14 + 10 + 5 = 50$. The counts are correct now.
Here is the grouped frequency distribution table:
| Heights (in cm) | Number of Students (Frequency) |
| 150 - 155 | 12 |
| 155 - 160 | 9 |
| 160 - 165 | 14 |
| 165 - 170 | 10 |
| 170 - 175 | 5 |
| Total | 50 |
(ii) What can you conclude about their heights from the table?
From the grouped frequency distribution table, we can observe the following features about the students' heights:
1. The height of most students lies in the class interval 160 - 165 cm, as it has the maximum frequency of 14.
2. A large number of students have heights between 160 cm and 170 cm ($14 + 10 = 24$ students).
3. The number of students with heights below 160 cm is $12 + 9 = 21$.
4. The number of students with heights 165 cm or more is $10 + 5 = 15$.
5. The heights are distributed across the range from 150 cm to 175 cm.
Question 5. A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:
| 0.03 | 0.08 | 0.08 | 0.09 | 0.04 | 0.17 |
| 0.16 | 0.05 | 0.02 | 0.06 | 0.18 | 0.20 |
| 0.11 | 0.08 | 0.12 | 0.13 | 0.22 | 0.07 |
| 0.08 | 0.01 | 0.10 | 0.06 | 0.09 | 0.18 |
| 0.11 | 0.07 | 0.05 | 0.07 | 0.01 | 0.04 |
(i) Make a grouped frequency distribution table for this data with class intervals as 0.00 - 0.04, 0.04 - 0.08, and so on.
(ii) For how many days, was the concentration of sulphur dioxide more than 0.11 parts per million?
Answer:
(i) Grouped Frequency Distribution Table
To create the grouped frequency distribution table for the given data, we will use the specified class intervals: 0.00 - 0.04, 0.04 - 0.08, and so on. We assume that the upper limit of each class is not included in the interval (e.g., 0.04 is included in 0.04 - 0.08, not in 0.00 - 0.04).
The concentration of sulphur dioxide (in ppm) for 30 days is tallied as follows:
| Concentration of SO2 (in ppm) | Tally Marks | Frequency (Number of days) |
| 0.00 - 0.04 | $||||$ | 4 |
| 0.04 - 0.08 | $\bcancel{||||} \; ||||$ | 9 |
| 0.08 - 0.12 | $\bcancel{||||} \; ||||$ | 9 |
| 0.12 - 0.16 | $||$ | 2 |
| 0.16 - 0.20 | $||||$ | 4 |
| 0.20 - 0.24 | $||$ | 2 |
| Total | 30 |
(ii) Number of days with SO2 concentration more than 0.11 ppm
To find the number of days the concentration of sulphur dioxide was more than 0.11 ppm, we need to sum the frequencies of the class intervals that cover values greater than 0.11.
These intervals are:
- 0.12 - 0.16
- 0.16 - 0.20
- 0.20 - 0.24
From the frequency distribution table created in part (i), we have:
Frequency for the interval 0.12 - 0.16 = 2 days
Frequency for the interval 0.16 - 0.20 = 4 days
Frequency for the interval 0.20 - 0.24 = 2 days
Total number of days with concentration more than 0.11 ppm = Sum of frequencies of these intervals
Total days = $2 + 4 + 2 = 8$
Therefore, the concentration of sulphur dioxide was more than 0.11 parts per million for 8 days.
Question 6. Three coins were tossed 30 times simultaneously. Each time the number of heads occurring was noted down as follows:
| 0 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 3 | 0 |
| 1 | 3 | 1 | 1 | 2 | 2 | 0 | 1 | 2 | 1 |
| 3 | 0 | 0 | 1 | 1 | 2 | 3 | 2 | 2 | 0 |
Prepare a frequency distribution table for the data given above.
Answer:
To prepare the frequency distribution table, we need to count how many times each possible outcome (number of heads) occurred. The possible outcomes when tossing three coins are 0, 1, 2, or 3 heads.
By counting the occurrences of each number from the given data:
- The number 0 appears 6 times.
- The number 1 appears 10 times.
- The number 2 appears 9 times.
- The number 3 appears 5 times.
We can now construct the frequency distribution table using this information.
| Number of Heads | Tally Marks | Frequency (Number of times) |
| 0 | $\bcancel{||||} \; |$ | 6 |
| 1 | $\bcancel{||||} \; \bcancel{||||}$ | 10 |
| 2 | $\bcancel{||||} \; ||||$ | 9 |
| 3 | $\bcancel{||||}$ | 5 |
| Total | 30 |
Question 7. The value of π upto 50 decimal places is given below:
3.14159265358979323846264338327950288419716939937510
(i) Make a frequency distribution of the digits from 0 to 9 after the decimal point.
(ii) What are the most and the least frequently occurring digits?
Answer:
Given:
The value of $\pi$ upto 50 decimal places is 3.14159265358979323846264338327950288419716939937510.
We are concerned with the 50 digits after the decimal point:
1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 4, 6, 2, 6, 4, 3, 3, 8, 3, 2, 7, 9, 5, 0, 2, 8, 8, 4, 1, 9, 7, 1, 6, 9, 3, 9, 9, 3, 7, 5, 1, 0.
(i) To Make:
A frequency distribution of the digits from 0 to 9 after the decimal point.
Solution (i):
We count the occurrence of each digit (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) in the 50 decimal places.
- Digit 0: appears 2 times.
- Digit 1: appears 5 times.
- Digit 2: appears 5 times.
- Digit 3: appears 8 times.
- Digit 4: appears 4 times.
- Digit 5: appears 5 times.
- Digit 6: appears 4 times.
- Digit 7: appears 4 times.
- Digit 8: appears 5 times.
- Digit 9: appears 8 times.
Total frequency = $2 + 5 + 5 + 8 + 4 + 5 + 4 + 4 + 5 + 8 = 50$.
Here is the frequency distribution table:
| Digit | Frequency |
| 0 | 2 |
| 1 | 5 |
| 2 | 5 |
| 3 | 8 |
| 4 | 4 |
| 5 | 5 |
| 6 | 4 |
| 7 | 4 |
| 8 | 5 |
| 9 | 8 |
| Total | 50 |
(ii) To Find:
The most and the least frequently occurring digits.
Solution (ii):
From the frequency distribution table:
The highest frequency is 8, which corresponds to the digits 3 and 9.
The lowest frequency is 2, which corresponds to the digit 0.
Therefore:
The most frequently occurring digits are 3 and 9.
The least frequently occurring digit is 0.
Question 8. Thirty children were asked about the number of hours they watched TV programmes in the previous week. The results were found as follows:
| 1 | 6 | 2 | 3 | 5 | 12 | 5 | 8 | 4 | 8 |
| 10 | 3 | 4 | 12 | 2 | 8 | 15 | 1 | 17 | 6 |
| 3 | 2 | 8 | 5 | 9 | 6 | 8 | 7 | 14 | 12 |
(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class intervals as 5 - 10.
(ii) How many children watched television for 15 or more hours a week?
Answer:
(i) Grouped Frequency Distribution Table
To create the grouped frequency distribution table, we are given a class width of 5 and one of the class intervals as 5 - 10. Based on the range of the data (from 1 to 17), the required class intervals are 0 - 5, 5 - 10, 10 - 15, and 15 - 20. We will assume that the lower limit of each class is included, and the upper limit is excluded (e.g., 5 is included in the 5-10 interval, but 10 is included in the 10-15 interval).
The frequency distribution table for the given data is as follows:
| Class Interval (Hours) | Tally Marks | Frequency (Number of Children) |
| 0 - 5 | $\bcancel{||||} \; \bcancel{||||}$ | 10 |
| 5 - 10 | $\bcancel{||||} \; \bcancel{||||} \; |||$ | 13 |
| 10 - 15 | $\bcancel{||||}$ | 5 |
| 15 - 20 | $||$ | 2 |
| Total | 30 |
(ii) Number of children who watched television for 15 or more hours a week
To find the number of children who watched TV for 15 or more hours, we look at the frequency of the class intervals that include 15 and above.
From the table, the class interval for "15 or more hours" is 15 - 20.
The number of children in this class interval is 2.
Therefore, 2 children watched television for 15 or more hours a week.
Question 9. A company manufactures car batteries of a particular type. The lives (in years) of 40 such batteries were recorded as follows:
| 2.6 | 3.0 | 3.7 | 3.2 | 2.2 | 4.1 | 3.5 | 4.5 |
| 3.5 | 2.3 | 3.2 | 3.4 | 3.8 | 3.2 | 4.6 | 3.7 |
| 2.5 | 4.4 | 3.4 | 3.3 | 2.9 | 3.0 | 4.3 | 2.8 |
| 3.5 | 3.2 | 3.9 | 3.2 | 3.2 | 3.1 | 3.7 | 3.4 |
| 4.6 | 3.8 | 3.2 | 2.6 | 3.5 | 4.2 | 2.9 | 3.6 |
Construct a grouped frequency distribution table for this data, using class intervals of size 0.5 starting from the interval 2 - 2.5.
Answer:
To construct the grouped frequency distribution table, we use the given class intervals with a size of 0.5, starting from 2.0 - 2.5. We tally the given data of the lives of 40 batteries into these classes. We assume the standard convention where the lower limit of a class is included, and the upper limit is excluded (e.g., a battery life of 2.5 years would be included in the 2.5 - 3.0 interval).
The grouped frequency distribution table is as follows:
| Class Interval (Life in years) | Tally Marks | Frequency (Number of batteries) |
| 2.0 - 2.5 | $||$ | 2 |
| 2.5 - 3.0 | $\bcancel{||||} \; |$ | 6 |
| 3.0 - 3.5 | $\bcancel{||||} \; \bcancel{||||} \; ||||$ | 14 |
| 3.5 - 4.0 | $\bcancel{||||} \; \bcancel{||||} \; |$ | 11 |
| 4.0 - 4.5 | $||||$ | 4 |
| 4.5 - 5.0 | $|||$ | 3 |
| Total | 40 |
Example 5 to 9 (Before Exercise 14.3)
Example 5. In a particular section of Class IX, 40 students were asked about the months of their birth and the following graph was prepared for the data so obtained:
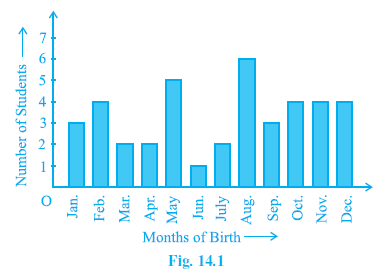
Observe the bar graph given above and answer the following questions:
(i) How many students were born in the month of November?
(ii) In which month were the maximum number of students born?
Answer:
(i) How many students were born in the month of November?
To answer this question, we observe the bar graph and locate the bar corresponding to the month of November on the horizontal axis (Months of Birth).
The height of the bar for November corresponds to the value on the vertical axis (Number of Students). Following the top of the bar for November to the left, we can see that it aligns with the number 4.
Therefore, 4 students were born in the month of November.
(ii) In which month were the maximum number of students born?
To find the month with the maximum number of births, we need to identify the tallest bar in the graph, as the height of the bar represents the number of students.
By observing the graph, the tallest bar corresponds to the month of August. The height of this bar reaches 6, which is the highest value among all the months.
Therefore, the maximum number of students were born in the month of August.
Example 6. A family with a monthly income of ₹ 20,000 had planned the following expenditures per month under various heads:
Table 14.5
| Heads | Expenditure (in thousand rupees) |
|---|---|
| Grocery | 4 |
| Rent | 5 |
| Education of children | 5 |
| Medicine | 2 |
| Fuel | 2 |
| Entertainment | 1 |
| Miscellaneous | 1 |
Draw a bar graph for the data above.
Answer:
Given
Monthly expenditures of a family under various heads:
| Heads | Expenditure (in thousand $\textsf{₹}$) |
| Grocery | 4 |
| Rent | 5 |
| Education of children | 5 |
| Medicine | 2 |
| Fuel | 2 |
| Entertainment | 1 |
| Miscellaneous | 1 |
To Draw
A bar graph for the given data.
Steps for Construction
1. Draw two perpendicular axes, the horizontal axis (x-axis) and the vertical axis (y-axis).
2. On the horizontal axis, represent the 'Heads' (categories of expenditure). Leave uniform space between the bars.
3. On the vertical axis, represent the 'Expenditure (in thousand $\textsf{₹}$)'. Since the maximum expenditure is 5 thousand rupees, we can choose a scale where 1 unit on the y-axis represents 1 thousand rupees. Mark the y-axis from 0 up to a value slightly greater than 5 (e.g., 6).
4. For each 'Head', draw a bar of uniform width. The height of each bar should correspond to the expenditure value for that head on the vertical axis.
- For 'Grocery', draw a bar of height 4 units.
- For 'Rent', draw a bar of height 5 units.
- For 'Education of children', draw a bar of height 5 units.
- For 'Medicine', draw a bar of height 2 units.
- For 'Fuel', draw a bar of height 2 units.
- For 'Entertainment', draw a bar of height 1 unit.
- For 'Miscellaneous', draw a bar of height 1 unit.
5. Label the axes: 'Heads of Expenditure' on the x-axis and 'Expenditure (in thousand $\textsf{₹}$)' on the y-axis.
6. Give a suitable title to the bar graph, e.g., "Monthly Expenditure of a Family".
The resulting bar graph is shown below:
Example 7. A teacher wanted to analyse the performance of two sections of students in a mathematics test of 100 marks. Looking at their performances, she found that a few students got under 20 marks and a few got 70 marks or above. So she decided to group them into intervals of varying sizes as follows: 0 - 20, 20 - 30, . . ., 60 - 70, 70 - 100. Then she formed the following table:
Table 14.7
| Marks | Number of students |
|---|---|
| 0 - 20 | 7 |
| 20 - 30 | 10 |
| 30 - 40 | 10 |
| 40 - 50 | 20 |
| 50 - 60 | 20 |
| 60 - 70 | 15 |
| 70 - above | 8 |
| Total | 90 |
Draw a histogram corresponding to this frequency distribution table provided above.
Answer:
Given
A grouped frequency distribution table showing the marks obtained by 90 students in a mathematics test, with unequal class widths.
| Marks | Number of students (Frequency) |
| 0 - 20 | 7 |
| 20 - 30 | 10 |
| 30 - 40 | 10 |
| 40 - 50 | 20 |
| 50 - 60 | 20 |
| 60 - 70 | 15 |
| 70 - 100 | 8 |
| Total | 90 |
To Draw
A histogram for the given data.
Solution
Since the class widths in the given frequency distribution table are unequal, the heights of the rectangles in the histogram must be adjusted to be proportional to the frequency.
The formula for the adjusted height of the rectangle is:
Adjusted Frequency = $\frac{\text{Frequency of the class}}{\text{Width of the class}} \times \text{Minimum Class Width}$
First, we find the width of each class interval:
The class widths are 20, 10, 10, 10, 10, 10, and 30. The minimum class width is 10.
Now, we calculate the adjusted frequency for each class:
| Marks | Class Width | Frequency | Adjusted Frequency ($\frac{\text{Frequency}}{\text{Width}} \times 10$) |
| 0 - 20 | 20 | 7 | $\frac{7}{20} \times 10 = 3.5$ |
| 20 - 30 | 10 | 10 | $\frac{10}{10} \times 10 = 10.0$ |
| 30 - 40 | 10 | 10 | $\frac{10}{10} \times 10 = 10.0$ |
| 40 - 50 | 10 | 20 | $\frac{20}{10} \times 10 = 20.0$ |
| 50 - 60 | 10 | 20 | $\frac{20}{10} \times 10 = 20.0$ |
| 60 - 70 | 10 | 15 | $\frac{15}{10} \times 10 = 15.0$ |
| 70 - 100 | 30 | 8 | $\frac{8}{30} \times 10 = \frac{8}{3} \approx 2.67$ |
Steps for Drawing the Histogram
1. Represent the 'Marks' on the x-axis and the 'Adjusted Frequency' on the y-axis.
2. Draw adjacent rectangles for each class interval. The width of each rectangle is its class width, and the height is its adjusted frequency.
The resulting histogram is shown below:
Example 8. Consider the marks, out of 100, obtained by 51 students of a class in a test, given in Table 14.9.
Table 14.9
| Marks | Number of students |
|---|---|
| 0 - 10 | 5 |
| 10 - 20 | 10 |
| 20 - 30 | 4 |
| 30 - 40 | 6 |
| 40 - 50 | 7 |
| 50 - 60 | 3 |
| 60 - 70 | 2 |
| 70 - 80 | 2 |
| 80 - 90 | 3 |
| 90 - 100 | 9 |
| Total | 51 |
Draw a frequency polygon corresponding to this frequency distribution table.
Answer:
Given
A frequency distribution table showing the marks obtained by 51 students.
| Marks | Number of students (Frequency) |
| 0 - 10 | 5 |
| 10 - 20 | 10 |
| 20 - 30 | 4 |
| 30 - 40 | 6 |
| 40 - 50 | 7 |
| 50 - 60 | 3 |
| 60 - 70 | 2 |
| 70 - 80 | 2 |
| 80 - 90 | 3 |
| 90 - 100 | 9 |
| Total | 51 |
To Draw
A frequency polygon for the given data.
Solution
To draw a frequency polygon, we first need to find the mid-point (class mark) of each class interval. The mid-point is calculated as $\frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
We then plot the points (Class Mark, Frequency) and connect them.
Let's prepare the table with class marks:
| Marks | Class Mark | Frequency |
| 0 - 10 | 5 | 5 |
| 10 - 20 | 15 | 10 |
| 20 - 30 | 25 | 4 |
| 30 - 40 | 35 | 6 |
| 40 - 50 | 45 | 7 |
| 50 - 60 | 55 | 3 |
| 60 - 70 | 65 | 2 |
| 70 - 80 | 75 | 2 |
| 80 - 90 | 85 | 3 |
| 90 - 100 | 95 | 9 |
To close the polygon, we consider two imaginary classes with zero frequency: one before the first class (-10 to 0) and one after the last class (100 to 110). Their class marks are -5 and 105, respectively.
The points to be plotted are: (-5, 0), (5, 5), (15, 10), (25, 4), (35, 6), (45, 7), (55, 3), (65, 2), (75, 2), (85, 3), (95, 9), and (105, 0).
Steps for Drawing the Frequency Polygon
1. Represent the 'Marks' (Class Marks) on the x-axis and the 'Number of Students' (Frequency) on the y-axis.
2. Plot the points calculated above.
3. Join these points with straight line segments to form the frequency polygon.
The resulting frequency polygon is shown below:
Example 9. In a city, the weekly observations made in a study on the cost of living index are given in the following table:
Table 14.10
| Cost of living index | Number of weeks |
|---|---|
| 140 - 150 | 5 |
| 150 - 160 | 10 |
| 160 - 170 | 20 |
| 170 - 180 | 9 |
| 180 - 190 | 6 |
| 190 - 200 | 2 |
| Total | 52 |
Draw a frequency polygon corresponding to this frequency distribution table.
Answer:
Given
A frequency distribution table showing the cost of living index and the number of weeks.
| Cost of living index | Number of weeks (Frequency) |
| 140 - 150 | 5 |
| 150 - 160 | 10 |
| 160 - 170 | 20 |
| 170 - 180 | 9 |
| 180 - 190 | 6 |
| 190 - 200 | 2 |
| Total | 52 |
To Draw
A frequency polygon for the given data.
Solution
To draw a frequency polygon, we first find the mid-point (class mark) of each class interval using the formula: Mid-point = $\frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
Let's calculate the class marks and prepare the table for plotting:
| Class Interval | Class Mark (Mid-point) | Frequency |
| 140 - 150 | 145 | 5 |
| 150 - 160 | 155 | 10 |
| 160 - 170 | 165 | 20 |
| 170 - 180 | 175 | 9 |
| 180 - 190 | 185 | 6 |
| 190 - 200 | 195 | 2 |
To complete the polygon, we consider imaginary classes with zero frequency before the first class (130-140) and after the last class (200-210). Their class marks are 135 and 205, respectively.
The points to be plotted on the graph are (Class Mark, Frequency): (135, 0), (145, 5), (155, 10), (165, 20), (175, 9), (185, 6), (195, 2), and (205, 0).
Steps for Drawing the Frequency Polygon
1. Represent the 'Cost of living index' (Class Marks) on the x-axis and the 'Number of weeks' (Frequency) on the y-axis.
2. Plot the points listed above.
3. Join these points with straight line segments to get the required frequency polygon.
The resulting frequency polygon is shown below:
Exercise 14.3
Question 1. A survey conducted by an organisation for the cause of illness and death among the women between the ages 15 - 44 (in years) worldwide, found the following figures (in %):
| S.No. | Causes | Female fatality rate (%) |
|---|---|---|
| 1. | Reproductive health conditions | 31.8 |
| 2. | Neuropsychiatric conditions | 25.4 |
| 3. | Injuries | 12.4 |
| 4. | Cardiovascular conditions | 4.3 |
| 5. | Respiratory conditions | 4.1 |
| 6. | Other causes | 22.0 |
(i) Represent the information given above graphically.
(ii) Which condition is the major cause of women’s ill health and death worldwide?
(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Answer:
Given
The percentage of female fatality rates for various causes among women aged 15-44 worldwide.
| S.No. | Causes | Female fatality rate (%) |
| 1. | Reproductive health conditions | 31.8 |
| 2. | Neuropsychiatric conditions | 25.4 |
| 3. | Injuries | 12.4 |
| 4. | Cardiovascular conditions | 4.3 |
| 5. | Respiratory conditions | 4.1 |
| 6. | Other causes | 22.0 |
(i) Represent the information given above graphically.
A bar graph is a suitable way to represent this data. We represent the 'Causes' on the horizontal axis and the 'Female fatality rate (%)' on the vertical axis.
(ii) Which condition is the major cause of women’s ill health and death worldwide?
From the given table and the bar graph, the highest female fatality rate is 31.8%, which corresponds to 'Reproductive health conditions'.
Therefore, the major cause of women’s ill health and death worldwide (in the age group 15-44) is Reproductive health conditions.
(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Two factors that play a major role in 'Reproductive health conditions' being the major cause of women's ill health and death worldwide in the age group 15-44 could be:
1. Lack of access to adequate healthcare facilities and services: Many women, especially in developing regions, lack access to timely and quality healthcare, including antenatal care, safe delivery services, and postnatal care. This leads to preventable complications during pregnancy, childbirth, and postpartum periods becoming fatal.
2. Lack of awareness and education on reproductive health: Limited access to information about sexual and reproductive health, family planning, and hygiene practices contributes to a higher incidence of reproductive tract infections, complications from unsafe abortions, and difficulties in managing pregnancy-related issues effectively.
Question 2. The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below.
| Section | Number of girls per thousand boys |
|---|---|
| Scheduled Caste (SC) | 940 |
| Scheduled Tribe (ST) | 970 |
| Non SC/ST | 920 |
| Backward districts | 950 |
| Non - backward districts | 920 |
| Rural | 930 |
| Urban | 910 |
(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Answer:
Given
Number of girls per thousand boys in different sections of Indian society.
| Section | Number of girls per thousand boys |
| Scheduled Caste (SC) | 940 |
| Scheduled Tribe (ST) | 970 |
| Non SC/ST | 920 |
| Backward districts | 950 |
| Non - backward districts | 920 |
| Rural | 930 |
| Urban | 910 |
(i) Represent the information above by a bar graph.
We use a bar graph to display the data, with 'Section' on the horizontal axis and 'Number of girls per thousand boys' on the vertical axis.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Based on the bar graph, several conclusions can be discussed:
1. Sex Ratio Imbalance: In all sections represented, the number of girls per thousand boys is less than 1000. This indicates a skewed sex ratio across the board, with fewer females than males.
2. Comparison Across Sections:
- The sex ratio is highest among Scheduled Tribes (ST) (970), suggesting a relatively better status for girls in this section compared to others.
- The sex ratio is lowest in Urban areas (910). This might be counter-intuitive as one might expect better conditions in urban settings, leading to discussions about the prevalence of practices like sex-selective abortions.
- The sex ratio in Backward districts (950) is higher than in Non-backward districts (920). Similarly, Rural areas (930) have a better sex ratio than Urban areas (910).
3. Areas of Concern: The low sex ratio in Urban areas and among Non SC/ST populations highlights these as key areas for intervention and awareness campaigns to improve the value and survival of the girl child.
Question 3. Given below are the seats won by different political parties in the polling outcome of a state assembly elections:
| Political Party | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Seats Won | 75 | 55 | 37 | 29 | 10 | 37 |
(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Answer:
Given
The number of seats won by different political parties in a state assembly election.
| Political Party | Seats Won |
| A | 75 |
| B | 55 |
| C | 37 |
| D | 29 |
| E | 10 |
| F | 37 |
(i) Draw a bar graph to represent the polling results.
A bar graph is used to represent the polling results, with the political parties on the x-axis and the number of seats won on the y-axis.
(ii) Which political party won the maximum number of seats?
By observing the data in the table or the heights of the bars in the graph, we can find the party with the maximum number of seats.
The highest number of seats won is 75.
Therefore, Political Party A won the maximum number of seats.
Question 4. The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table:
| Length (in mm) | Number of leaves |
|---|---|
| 118 - 126 | 3 |
| 127 - 135 | 5 |
| 136 - 144 | 9 |
| 145 - 153 | 12 |
| 154 - 162 | 5 |
| 163 - 171 | 4 |
| 172 - 180 | 2 |
(i) Draw a histogram to represent the given data. [Hint: First make the class intervals continuous]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
Answer:
Given
The length of 40 leaves (in mm) and their frequency distribution.
(i) Draw a histogram to represent the given data.
The class intervals are discontinuous. To draw a histogram, we must first make them continuous. The gap between consecutive classes is $127 - 126 = 1$. We add and subtract half of this gap (0.5) to the upper and lower limits, respectively.
The new continuous class intervals are:
| Length (in mm) (Continuous) | Number of leaves (Frequency) |
| 117.5 - 126.5 | 3 |
| 126.5 - 135.5 | 5 |
| 135.5 - 144.5 | 9 |
| 144.5 - 153.5 | 12 |
| 153.5 - 162.5 | 5 |
| 162.5 - 171.5 | 4 |
| 171.5 - 180.5 | 2 |
Now we can draw the histogram using these continuous intervals on the x-axis and the frequencies on the y-axis.
(ii) Is there any other suitable graphical representation for the same data?
Yes, a Frequency Polygon is another suitable graphical representation for this data. It can be constructed by joining the mid-points of the tops of the bars of the histogram.
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
No, this conclusion is incorrect.
Reason: The data is presented in groups. The class interval 145 - 153 (or 144.5 - 153.5) has the highest frequency of 12. This only means that the 12 leaves with the most common lengths have lengths that fall *somewhere* within this range. We do not know the exact individual lengths of these 12 leaves from the given table. Therefore, we cannot conclude that their length is exactly 153 mm.
Question 5. The following table gives the life times of 400 neon lamps:
| Life time (in hours) | Number of lamps |
|---|---|
| 300 - 400 | 14 |
| 400 - 500 | 56 |
| 500 - 600 | 60 |
| 600 - 700 | 86 |
| 700 - 800 | 74 |
| 800 - 900 | 62 |
| 900 - 1000 | 48 |
(i) Represent the given information with the help of a histogram.
(ii) How many lamps have a life time of more than 700 hours?
Answer:
Given
The life times (in hours) of 400 neon lamps.
| Life time (in hours) | Number of lamps (Frequency) |
| 300 - 400 | 14 |
| 400 - 500 | 56 |
| 500 - 600 | 60 |
| 600 - 700 | 86 |
| 700 - 800 | 74 |
| 800 - 900 | 62 |
| 900 - 1000 | 48 |
(i) Represent the given information with the help of a histogram.
The class intervals are continuous and have a uniform width. We can draw the histogram with 'Life time' on the x-axis and 'Number of lamps' on the y-axis.
(ii) How many lamps have a life time of more than 700 hours?
To find the number of lamps with a lifetime of more than 700 hours, we need to sum the frequencies of the class intervals from 700-800 onwards.
Number of lamps = (Frequency of 700-800) + (Frequency of 800-900) + (Frequency of 900-1000)
Number of lamps = $74 + 62 + 48 = 184$
Therefore, 184 lamps have a life time of more than 700 hours.
Question 6. The following table gives the distribution of students of two sections according to the marks obtained by them:
| Section A | Section B | ||
| Marks | Frequency | Marks | Frequency |
| 0 - 10 | 3 | 0 - 10 | 5 |
| 10 - 20 | 9 | 10 - 20 | 19 |
| 20 - 30 | 17 | 20 - 30 | 15 |
| 30 - 40 | 12 | 30 - 40 | 10 |
| 40 - 50 | 9 | 40 - 50 | 1 |
Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Answer:
Given
Frequency distribution of marks for two sections (A and B).
Solution
To draw the frequency polygons, we first need to find the mid-points (class marks) of the class intervals.
| Marks | Class Mark | Frequency (Section A) | Frequency (Section B) |
| 0 - 10 | 5 | 3 | 5 |
| 10 - 20 | 15 | 9 | 19 |
| 20 - 30 | 25 | 17 | 15 |
| 30 - 40 | 35 | 12 | 10 |
| 40 - 50 | 45 | 9 | 1 |
We plot the class marks on the x-axis and the frequencies on the y-axis for both sections and join the points with line segments. To close the polygons, we use class marks of preceding (-5) and succeeding (55) intervals with zero frequency.
Comparison of Performance
By observing the two frequency polygons on the graph:
1. The peak of Section B's polygon is higher in the 10-20 marks range, indicating a large number of students scored in this lower range.
2. The peak of Section A's polygon is in the 20-30 marks range. Overall, the polygon for Section A is shifted more towards the right (higher marks) compared to Section B.
3. Section A has a significantly higher number of students scoring more than 20 marks compared to Section B.
Conclusion: The performance of Section A is better than that of Section B, as more students in Section A have scored higher marks.
Question 7. The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:
| Number of balls | Team A | Team B |
|---|---|---|
| 1 - 6 | 2 | 5 |
| 7 - 12 | 1 | 6 |
| 13 - 18 | 8 | 2 |
| 19 - 24 | 9 | 10 |
| 25 - 30 | 4 | 5 |
| 31 - 36 | 5 | 6 |
| 37 - 42 | 6 | 3 |
| 43 - 48 | 10 | 4 |
| 49 - 54 | 6 | 8 |
| 55 - 60 | 2 | 10 |
Represent the data of both the teams on the same graph by frequency polygons.
[Hint: First make the class intervals continuous.]
Answer:
Given
Runs scored by two teams A and B in intervals of 6 balls.
Solution
First, we make the class intervals continuous by subtracting 0.5 from lower limits and adding 0.5 to upper limits. Then, we find the mid-point (class mark) of each continuous interval.
| Number of balls (Continuous) | Class Mark | Team A (Runs) | Team B (Runs) |
| 0.5 - 6.5 | 3.5 | 2 | 5 |
| 6.5 - 12.5 | 9.5 | 1 | 6 |
| 12.5 - 18.5 | 15.5 | 8 | 2 |
| 18.5 - 24.5 | 21.5 | 9 | 10 |
| 24.5 - 30.5 | 27.5 | 4 | 5 |
| 30.5 - 36.5 | 33.5 | 5 | 6 |
| 36.5 - 42.5 | 39.5 | 6 | 3 |
| 42.5 - 48.5 | 45.5 | 10 | 4 |
| 48.5 - 54.5 | 51.5 | 6 | 8 |
| 54.5 - 60.5 | 57.5 | 2 | 10 |
We plot these class marks on the x-axis and the runs on the y-axis for both teams on the same graph. To close the polygons, we use preceding (-2.5) and succeeding (63.5) class marks with zero frequency.
Question 8. A random survey of the number of children of various age groups playing in a park was found as follows:
| Age (in years) | Number of children |
|---|---|
| 1 - 2 | 5 |
| 2 - 3 | 3 |
| 3 - 5 | 6 |
| 5 - 7 | 12 |
| 7 - 10 | 9 |
| 10 - 15 | 10 |
| 15 - 17 | 4 |
Draw a histogram to represent the data above.
Answer:
Given
Frequency distribution of the number of children in various age groups.
Solution
The class intervals have unequal widths. To draw an accurate histogram, we must adjust the height of the rectangles. The height (or length) of each rectangle is calculated as:
Adjusted Frequency = $\frac{\text{Frequency}}{\text{Class Width}} \times \text{Minimum Class Width}$
The minimum class width is 1 (for 1-2 and 2-3).
| Age (in years) | Class Width | Frequency | Adjusted Frequency |
| 1 - 2 | 1 | 5 | $\frac{5}{1} \times 1 = 5$ |
| 2 - 3 | 1 | 3 | $\frac{3}{1} \times 1 = 3$ |
| 3 - 5 | 2 | 6 | $\frac{6}{2} \times 1 = 3$ |
| 5 - 7 | 2 | 12 | $\frac{12}{2} \times 1 = 6$ |
| 7 - 10 | 3 | 9 | $\frac{9}{3} \times 1 = 3$ |
| 10 - 15 | 5 | 10 | $\frac{10}{5} \times 1 = 2$ |
| 15 - 17 | 2 | 4 | $\frac{4}{2} \times 1 = 2$ |
We now draw the histogram using the class intervals for the width of the bars and the adjusted frequencies for the height of the bars.
Question 9. 100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:
| Number of letters | Number of surnames |
|---|---|
| 1 - 4 | 6 |
| 4 - 6 | 30 |
| 6 - 8 | 44 |
| 8 - 12 | 16 |
| 12 - 20 | 4 |
(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Answer:
Given
Frequency distribution of the number of letters in 100 surnames.
(i) Draw a histogram to depict the given information.
The class intervals have unequal widths, so we must calculate the adjusted frequencies to draw the histogram correctly. The minimum class width is 2 (for 4-6 and 6-8).
Adjusted Frequency = $\frac{\text{Frequency}}{\text{Class Width}} \times \text{Minimum Class Width}$
| Number of letters | Class Width | Frequency | Adjusted Frequency |
| 1 - 4 | 3 | 6 | $\frac{6}{3} \times 2 = 4$ |
| 4 - 6 | 2 | 30 | $\frac{30}{2} \times 2 = 30$ |
| 6 - 8 | 2 | 44 | $\frac{44}{2} \times 2 = 44$ |
| 8 - 12 | 4 | 16 | $\frac{16}{4} \times 2 = 8$ |
| 12 - 20 | 8 | 4 | $\frac{4}{8} \times 2 = 1$ |
We draw the histogram using the class intervals for the width and the adjusted frequencies for the height.
(ii) Write the class interval in which the maximum number of surnames lie.
To answer this, we look at the original frequency column in the given table, not the adjusted frequency.
The highest frequency is 44.
Therefore, the class interval in which the maximum number of surnames lie is 6 - 8.
Example 10 to 15 (Before Exercise 14.4)
Example 10. 5 people were asked about the time in a week they spend in doing social work in their community. They said 10, 7, 13, 20 and 15 hours, respectively. Find the mean (or average) time in a week devoted by them for social work.
Answer:
Given:
The time (in hours) spent by 5 people in a week doing social work: 10, 7, 13, 20, 15.
Number of observations, $n = 5$.
To Find:
The mean (average) time spent per week.
Solution:
The mean of ungrouped data is calculated by the formula:
$ \text{Mean} (\overline{x}) = \frac{\text{Sum of all observations}}{\text{Number of observations}} $
Sum of all observations = $10 + 7 + 13 + 20 + 15$
Sum of all observations = $65$
Number of observations, $n = 5$
Mean $(\overline{x}) = \frac{65}{5}$
Mean $(\overline{x}) = 13$
Alternatively, we can show the addition:
Sum of observations = $10 + 7 + 13 + 20 + 15$
Sum of observations = 65
Mean $(\overline{x}) = \frac{65}{5} = 13$
The mean time in a week devoted by them for social work is 13 hours.
Example 11. Find the mean of the marks obtained by 30 students of Class IX of a school, given in Example 2.
Answer:
Given
The marks obtained by 30 students of Class IX, as presented in the frequency distribution table from Example 2 of the textbook.
| Marks ($x_i$) | Number of Students ($f_i$) |
| 10 | 1 |
| 20 | 1 |
| 36 | 3 |
| 40 | 4 |
| 50 | 3 |
| 56 | 2 |
| 60 | 4 |
| 70 | 4 |
| 72 | 1 |
| 80 | 1 |
| 88 | 2 |
| 92 | 3 |
| 95 | 1 |
| Total | $\sum\limits f_i = 30$ |
To Find
The mean of the marks obtained by the 30 students.
Solution
To find the mean of the given data, we use the formula for the mean of data presented with frequencies:
$\text{Mean} (\overline{x}) = \frac{\sum\limits_{i=1}^{n} f_i x_i}{\sum\limits_{i=1}^{n} f_i}$
We first need to calculate the product of each mark ($x_i$) and its corresponding frequency ($f_i$), which is $f_i x_i$. Then, we find the sum of these products ($\sum\limits f_i x_i$).
Let's create a table to organize the calculations:
| Marks ($x_i$) | Number of Students ($f_i$) | $f_i x_i$ |
| 10 | 1 | $1 \times 10 = 10$ |
| 20 | 1 | $1 \times 20 = 20$ |
| 36 | 3 | $3 \times 36 = 108$ |
| 40 | 4 | $4 \times 40 = 160$ |
| 50 | 3 | $3 \times 50 = 150$ |
| 56 | 2 | $2 \times 56 = 112$ |
| 60 | 4 | $4 \times 60 = 240$ |
| 70 | 4 | $4 \times 70 = 280$ |
| 72 | 1 | $1 \times 72 = 72$ |
| 80 | 1 | $1 \times 80 = 80$ |
| 88 | 2 | $2 \times 88 = 176$ |
| 92 | 3 | $3 \times 92 = 276$ |
| 95 | 1 | $1 \times 95 = 95$ |
| Total | $\sum\limits f_i = 30$ | $\sum\limits f_i x_i = 1779$ |
From the table, we have:
Total number of students, $\sum\limits f_i = 30$
Sum of the products, $\sum\limits f_i x_i = 1779$
Now, we can calculate the mean:
Mean ($\overline{x}$) = $\frac{\sum\limits f_i x_i}{\sum\limits f_i} = \frac{1779}{30}$
Mean ($\overline{x}$) = 59.3
Thus, the mean of the marks obtained by the 30 students is 59.3.
Example 12. The heights (in cm) of 9 students of a class are as follows:
| 155 | 160 | 145 | 149 | 150 | 147 | 152 | 144 | 148 |
Answer:
Given
The heights (in cm) of 9 students of a class are:
155, 160, 145, 149, 150, 147, 152, 144, 148.
To Find
The median of the given data.
Solution
First, we arrange the given data in ascending order to find the median.
Arranging the heights in ascending order:
144, 145, 147, 148, 149, 150, 152, 155, 160
The number of observations is $n = 9$, which is an odd number.
When the number of observations is odd, the median is the middlemost value, which is the $(\frac{n+1}{2})^{th}$ observation.
Median position = $(\frac{9+1}{2})^{th}$ observation = $(\frac{10}{2})^{th}$ observation = $5^{th}$ observation.
Now, we find the 5th value in the arranged data:
144, 145, 147, 148, 149, 150, 152, 155, 160
The 5th observation is 149.
Therefore, the median height of the students is 149 cm.
Example 13. The points scored by a Kabaddi team in a series of matches are as follows:
| 17 | 2 | 7 | 27 | 15 | 5 | 14 | 8 | 10 | 24 | 48 | 10 | 8 | 7 | 18 | 28 |
Find the median of the points scored by the team.
Answer:
Given
The points scored by a Kabaddi team in a series of matches:
17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28.
To Find
The median of the points scored.
Solution
To find the median, we first arrange the data in ascending order.
Arranged data:
2, 5, 7, 7, 8, 8, 10, 10, 14, 15, 17, 18, 24, 27, 28, 48
The number of observations is $n = 16$, which is an even number.
When the number of observations is even, the median is the average of the two middle observations, which are the $(\frac{n}{2})^{th}$ and $(\frac{n}{2} + 1)^{th}$ observations.
$(\frac{16}{2})^{th}$ observation = $8^{th}$ observation.
$(\frac{16}{2} + 1)^{th}$ observation = $9^{th}$ observation.
From the arranged data:
The 8th observation is 10.
The 9th observation is 14.
Median = $\frac{8^{th} \text{ observation} + 9^{th} \text{ observation}}{2}$
Median = $\frac{10 + 14}{2} = \frac{24}{2} = 12$
The median of the points scored by the team is 12.
Example 14. Find the mode of the following marks (out of 10) obtained by 20 students:
| 4 | 6 | 5 | 9 | 3 | 2 | 7 | 7 | 6 | 5 | 4 | 9 | 10 | 10 | 3 | 4 | 7 | 6 | 9 | 9 |
Answer:
Given
The marks obtained by 20 students (out of 10):
4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9.
To Find
The mode of the marks.
Solution
The mode is the value that appears most frequently in a data set. To find the mode, let's create a frequency table for the marks.
| Mark | Frequency (Number of students) |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 2 |
| 6 | 3 |
| 7 | 3 |
| 9 | 4 |
| 10 | 2 |
By observing the frequency table, we can see that the mark '9' has the highest frequency of 4.
Therefore, the mode of the marks is 9.
Example 15. Consider a small unit of a factory where there are 5 employees : a supervisor and four labourers. The labourers draw a salary of ₹ 5,000 per month each while the supervisor gets ₹ 15,000 per month. Calculate the mean, median and mode of the salaries of this unit of the factory
Answer:
Given
Salaries of 5 employees in a factory unit:
- 4 labourers at $\textsf{₹}$ 5,000 per month each.
- 1 supervisor at $\textsf{₹}$ 15,000 per month.
The list of salaries is: $\textsf{₹}$ 5,000, $\textsf{₹}$ 5,000, $\textsf{₹}$ 5,000, $\textsf{₹}$ 5,000, $\textsf{₹}$ 15,000.
To Calculate
The mean, median, and mode of the salaries.
Solution
1. Calculation of Mean
Mean = $\frac{\text{Sum of all salaries}}{\text{Number of employees}}$
Sum of salaries = $(4 \times 5000) + 15000 = 20000 + 15000 = \textsf{₹}\ 35,000$
Number of employees = 5
Mean = $\frac{35000}{5} = \textsf{₹}\ 7,000$
The mean salary is $\textsf{₹}$ 7,000.
2. Calculation of Median
First, arrange the salaries in ascending order:
5000, 5000, 5000, 5000, 15000
The number of observations is $n = 5$ (odd). The median is the middle value, i.e., the $(\frac{n+1}{2})^{th}$ term.
Median position = $(\frac{5+1}{2}) = 3^{rd}$ term.
The 3rd term in the ordered list is 5000.
The median salary is $\textsf{₹}$ 5,000.
3. Calculation of Mode
The mode is the most frequently occurring value in the data.
In the list of salaries, the value $\textsf{₹}$ 5,000 appears 4 times, while $\textsf{₹}$ 15,000 appears only once.
The mode salary is $\textsf{₹}$ 5,000.
In this case, the mean ($\textsf{₹}$ 7,000) is influenced by the single high salary of the supervisor. The median and mode ($\textsf{₹}$ 5,000) better represent the typical salary of an employee in this unit.
Exercise 14.4
Question 1. The following number of goals were scored by a team in a series of 10 matches:
| 2 | 3 | 4 | 5 | 0 | 1 | 3 | 3 | 4 | 3 |
Find the mean, median and mode of these scores.
Answer:
Given
The number of goals scored by a team in 10 matches are:
2, 3, 4, 5, 0, 1, 3, 3, 4, 3.
Total number of matches (observations), $n = 10$.
To Find
The mean, median, and mode of these scores.
Solution
1. Mean
The mean is calculated using the formula:
Mean = $\frac{\text{Sum of all scores}}{\text{Total number of matches}}$
Sum of scores = $2 + 3 + 4 + 5 + 0 + 1 + 3 + 3 + 4 + 3 = 28$
Mean = $\frac{28}{10} = 2.8$
Therefore, the mean score is 2.8.
2. Median
To find the median, we first arrange the scores in ascending order:
0, 1, 2, 3, 3, 3, 4, 4, 5
Wait, there are only 9 scores here. Let's re-check the original data: 2, 3, 4, 5, 0, 1, 3, 3, 4, 3. There are four 3s. Let's reorder.
Ascending order: 0, 1, 2, 3, 3, 3, 3, 4, 4, 5
The number of observations is $n = 10$, which is an even number. The median is the average of the two middle values, which are the $(\frac{n}{2})^{th}$ and $(\frac{n}{2}+1)^{th}$ terms.
The 5th term is 3.
The 6th term is 3.
Median = $\frac{5^{th} \text{ term} + 6^{th} \text{ term}}{2} = \frac{3 + 3}{2} = \frac{6}{2} = 3$
Therefore, the median score is 3.
3. Mode
The mode is the score that appears most frequently.
From the arranged data (0, 1, 2, 3, 3, 3, 3, 4, 4, 5), we can see that the score '3' occurs 4 times, which is more than any other score.
Therefore, the mode of the scores is 3.
Question 2. In a mathematics test given to 15 students, the following marks (out of 100) are recorded:
| 41 | 39 | 48 | 52 | 46 | 62 | 54 | 40 | 96 | 52 | 98 | 40 | 42 | 52 | 60 |
Find the mean, median and mode of this data.
Answer:
Given
Marks obtained by 15 students:
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60.
Total number of students (observations), $n = 15$.
To Find
The mean, median, and mode of this data.
Solution
1. Mean
Mean = $\frac{\text{Sum of all marks}}{\text{Total number of students}}$
Sum of marks = $41 + 39 + 48 + 52 + 46 + 62 + 54 + 40 + 96 + 52 \ $$ + 98 + 40 + 42 + 52 + 60 = 822$
Mean = $\frac{822}{15} = 54.8$
Therefore, the mean mark is 54.8.
2. Median
First, we arrange the marks in ascending order:
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
The number of observations is $n = 15$, which is an odd number. The median is the middle value, i.e., the $(\frac{n+1}{2})^{th}$ term.
Median position = $(\frac{15+1}{2}) = 8^{th}$ term.
The 8th term in the ordered list is 52.
Therefore, the median mark is 52.
3. Mode
The mode is the mark that appears most frequently.
From the arranged data, we can count the frequency of each mark. The mark '52' appears 3 times, which is more than any other mark.
Therefore, the mode of the marks is 52.
Question 3. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x
| 29 | 32 | 48 | 50 | x | x + 2 | 72 | 78 | 84 | 95 |
Answer:
Given
The observations arranged in ascending order are:
29, 32, 48, 50, $x$, $x + 2$, 72, 78, 84, 95.
The total number of observations, $n = 10$.
The median of the data is 63.
To Find
The value of $x$.
Solution
Since the number of observations $n = 10$ is even, the median is the average of the two middle terms: the $(\frac{n}{2})^{th}$ term and the $(\frac{n}{2}+1)^{th}$ term.
5th term = $x$
6th term = $x + 2$
The formula for the median is:
Median = $\frac{5^{th} \text{ term} + 6^{th} \text{ term}}{2}$
Substituting the given values:
$63 = \frac{x + (x + 2)}{2}$
$63 = \frac{2x + 2}{2}$
$63 = x + 1$
$x = 63 - 1$
$x = 62$
Therefore, the value of $x$ is 62.
Question 4. Find the mode of 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
Answer:
Given
The data set is: 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
To Find
The mode of the data.
Solution
The mode is the value that occurs most frequently in a data set.
Let's count the frequency of each number in the given data:
- 14 appears 4 times.
- 25 appears 1 time.
- 28 appears 1 time.
- 18 appears 3 times.
- 17 appears 1 time.
- 23 appears 1 time.
- 22 appears 1 time.
The number 14 has the highest frequency (it appears 4 times).
Therefore, the mode of the given data is 14.
Question 5. Find the mean salary of 60 workers of a factory from the following table:
| Salary (in ₹) | Number of workers |
| 3000 | 16 |
| 4000 | 12 |
| 5000 | 10 |
| 6000 | 8 |
| 7000 | 6 |
| 8000 | 4 |
| 9000 | 3 |
| 10000 | 1 |
| Total | 60 |
Answer:
Given
A frequency distribution table of the salaries of 60 workers.
To Find
The mean salary of the 60 workers.
Solution
To find the mean salary, we use the formula $\overline{x} = \frac{\sum f_i x_i}{\sum f_i}$, where $x_i$ is the salary and $f_i$ is the number of workers.
We will create a calculation table:
| Salary (in $\textsf{₹}$) ($x_i$) | Number of workers ($f_i$) | $f_i x_i$ |
| 3000 | 16 | 48000 |
| 4000 | 12 | 48000 |
| 5000 | 10 | 50000 |
| 6000 | 8 | 48000 |
| 7000 | 6 | 42000 |
| 8000 | 4 | 32000 |
| 9000 | 3 | 27000 |
| 10000 | 1 | 10000 |
| Total | $\sum f_i = 60$ | $\sum f_i x_i = 305000$ |
From the table, we have:
Total number of workers, $\sum f_i = 60$.
Sum of products, $\sum f_i x_i = 305000$.
Now, we calculate the mean:
Mean Salary = $\frac{305000}{60} = \frac{30500}{6} \approx 5083.33$
The mean salary of the 60 workers is approximately $\textsf{₹}$ 5083.33.
Question 6. Give one example of a situation in which
(i) the mean is an appropriate measure of central tendency.
(ii) the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.
Answer:
(i) Situation where the mean is an appropriate measure of central tendency.
The mean is a good measure of central tendency when the data is symmetrically distributed and does not have extreme values (outliers).
Example: Consider the marks obtained by a student in 5 different subjects: 75, 80, 82, 85, 88. The data values are close to each other without any extreme scores.
Mean = $\frac{75+80+82+85+88}{5} = \frac{410}{5} = 82$.
Here, the mean mark of 82 provides a fair and accurate summary of the student's overall performance.
(ii) Situation where the mean is not appropriate, but the median is.
The mean is not a good measure when the data is skewed or contains extreme values (outliers), because the mean is heavily influenced by these outliers. In such cases, the median provides a better representation of the central value.
Example: Consider the monthly income of 5 employees in a small office: $\textsf{₹}$ 15,000, $\textsf{₹}$ 16,000, $\textsf{₹}$ 17,000, $\textsf{₹}$ 18,000, and $\textsf{₹}$ 1,00,000 (the owner's income).
Mean Income = $\frac{15000+16000+17000+18000+100000}{5} = \frac{166000}{5} = \textsf{₹}\ 33,200$.
This mean value of $\textsf{₹}$ 33,200 is not representative of what a typical employee earns, as it is much higher than the salary of 4 out of the 5 people.
Now let's find the median. The data is already in order. The median is the middle value (3rd term), which is $\textsf{₹}$ 17,000.
The median income of $\textsf{₹}$ 17,000 is a much better and more appropriate measure of the central tendency for this data, as it is not affected by the outlier salary of the owner.

